Spectral features
The Spectral features block extracts frequency, power and other characteristics of a signal. Low-pass and high-pass filters can also be applied to filter out unwanted frequencies. It is great for analyzing repetitive patterns in a signal, such as movements or vibrations from an accelerometer. It is also great for complex signals that have transients or irregular waveform, such as ECG and PPG signals.
GitHub repository containing all DSP block code: edgeimpulse/processing-blocks.
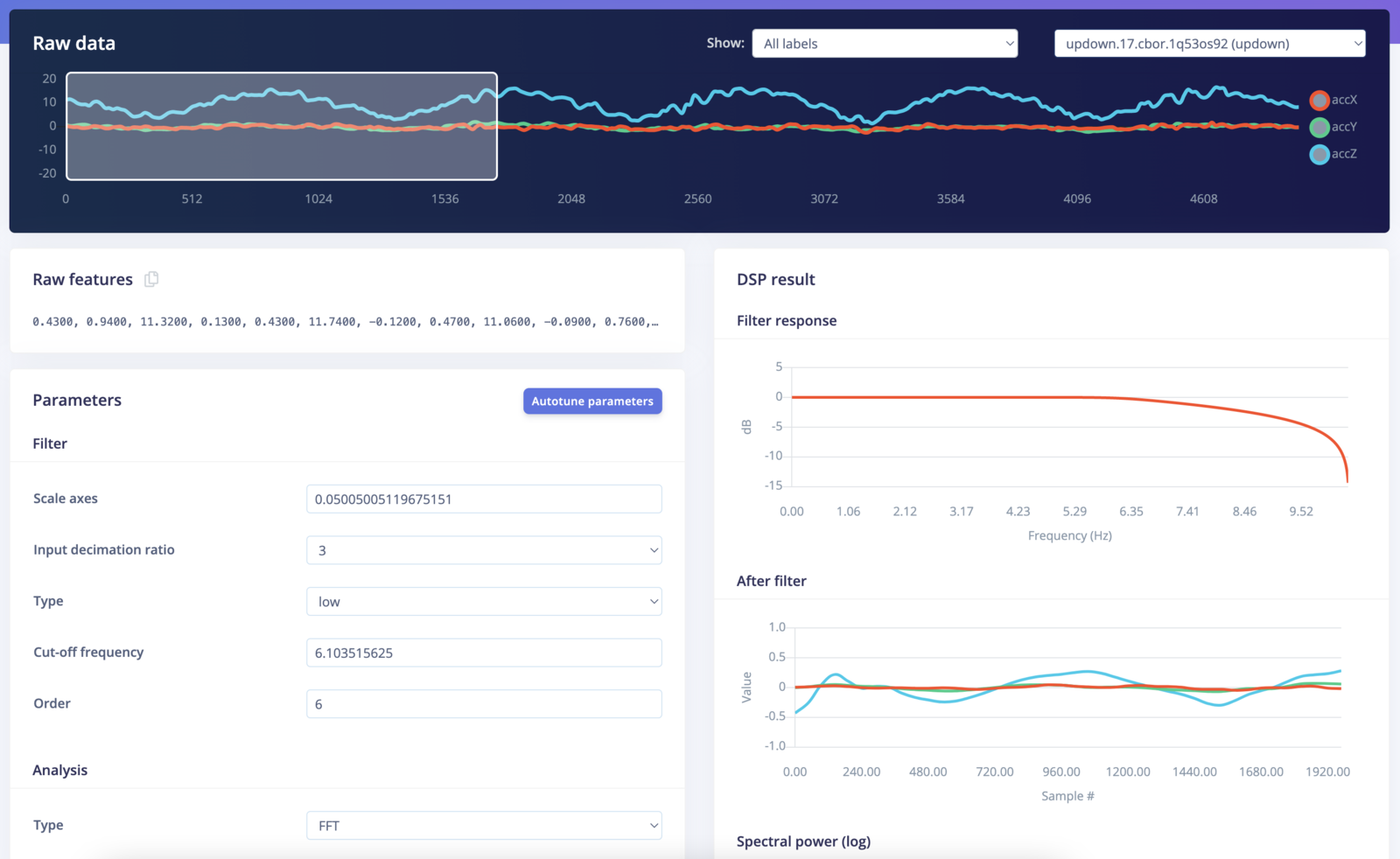
Spectral analysis parameters
Compatible with the DSP Autotuner
Picking the right parameters for DSP algorithms can be difficult. It often requires a lot of experience and experimenting. The autotuning function makes this process easier by looking at the entire dataset and recommending a set of parameters that is tuned for your dataset.
Filter
Prior to calculating the Fast Fourier Transform (FFT), the time-series data inside the window of your sample can be filtered, which often helps to smooth out the signal or drop unwanted artifacts. In the image above, a "window" is shown inside the white box; only the readings inside that box will be used for filtering and calculating the FFT.
Edge Impulse will slide the window over your sample, as given by the time series input block parameters during Impulse creation in order to generate several training/test samples from your longer time series sample.
Scale axes - Multiply all raw input values by this number.
Input decimation ratio - Decimating (downsampling) the signal reduces the number of features and improves frequency resolution in relevant bands without increasing resource usage.
Type - The type of filter to apply to the raw data (low-pass, high-pass, or none).
Cut-off frequency - Cut-off frequency of the filter in hertz. Also, this will remove unwanted frequency bins from the generated features.
Order - Order of the Butterworth filter. Must be an even number. A higher order has a sharper cutoff at the expense of latency. You can also set to zero, in which case, the signal won't be filtered, but unwanted frequency bins will still be removed from the output.
Removing frequency bins beyond the cut off reduces model size, which saves resources, and also leads to models that train well with less data
After filtering via a Butterworth IIR filter (if enabled), the mean is subtracted from the signal. Several statistical features (RMS, skewness, kurtosis) are calculated from the filtered signal after the mean has been removed. This filtered signal is passed to the Spectral power section, which computes the FFT in order to compute the spectral features.
Analysis - Spectral power
Analysis type - There are two types of analysis you can choose from.
FFT base analysis is best at analyzing repetitive patterns in a signal,
Wavelet works better for complex signals that have transients or irregular waveform.
If you are unsure which one to choose, using the autotuning function will give you a good starting point. After selecting an analysis type, relevant parameters will appear for the selected type.
FFT based analysis
This section controls how the FFT is applied to each filtered window from your sample. If the window from your sample is larger than the FFT size, then the window will be broken into frames (or "sub-windows"), and the FFT is calculated from each frame.
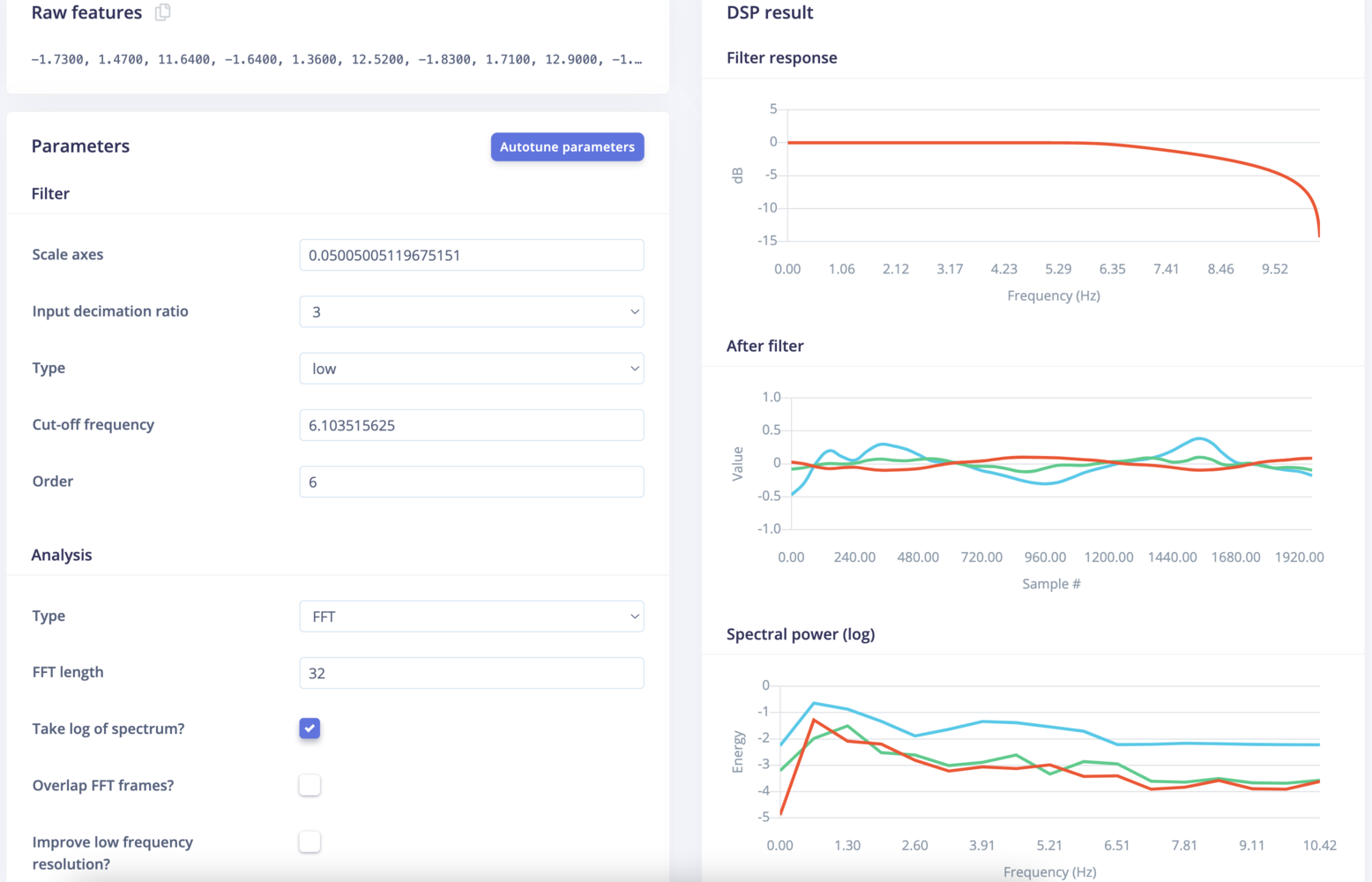
FFT length - The FFT size. This determines the number of FFT bins as well as the resolution of frequency peaks that you can separate. A lower number means more signals will average together in the same FFT bin, but also reduces the number of features and model size. A higher number will separate more signals into separate bins, but generates a larger model.
Take log of spectrum? - When selected, log (base 10) will be applied to each FFT bin. This gives more range to (ie, captures more information about) low intensity signals at the expense of range for higher intensity signals. It is enabled by default and is generally a good choice, but it ultimately depends on the kind if signal sampled.
Overlap FFT frames? - Successive frames (sub-windows) overlap by 1/2 within the larger window (given by the white box in the image) if this is checked. If unchecked, frames will not overlap. This "sliding frame" method can prevent transient events from being missed if they happen to appear on a frame boundary. Enabled by default. Disabling improves latency. No impact on model size or RAM usage.
Note that several FFTs will be computed, depending on the settings. For example, if you have 100 readings for a single axis in your window and set the FFT length to 16 with no overlap, then 6 FFTs will be computed (for that single axis), as we have 6 full frames (each with 16 points) that will fully cover those 100 readings/points.
For each FFT bin (i.e. range of frequencies), the maximum value from all of the frames is kept as the feature. Continuing with the example above, we throw away 1/2 of every FFT (as it's simply a mirror image of the other half). We also throw away the bin at 0 Hz (as we filter out the DC bias anyway when we subtracted the mean), but we keep the Nyquist bin. As a result, we end up with 8 usable bins from each of our 16-point FFTs. For each bin, we find the maximum value from our 6 FFTs that we computed (in that particular bin). So, the number of features would be 8.
Note that you may see fewer spectral features if you enable filtering, as we throw away any frequency bins higher than the cutoff frequency (for the low-pass filter) or lower than the cutoff frequency (for the high-pass filter).
See this video to learn more about the FFT.
Wavelet based analysis
This section controls how the wavelet based analysis is applied to your signal. We use the Discrete Wavelet Transform (DWT) to decompose a signal into multiple levels of approximations and details and then extract multiple features at each level.
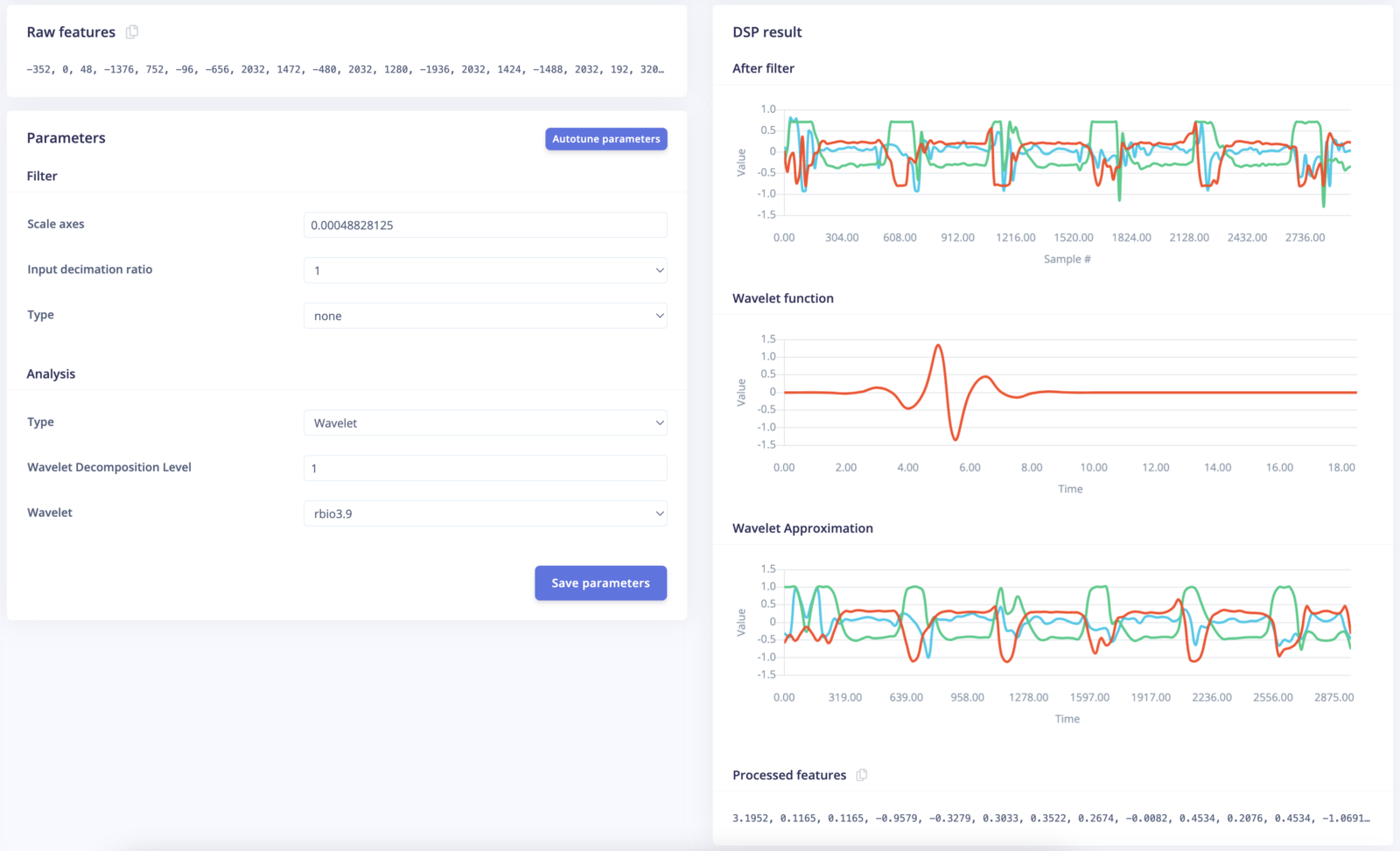
Wavelet decomposition level The level at which you wish to decompose the signal. Higher level reveals more information about the signal at a cost of more computing requirement and may introduce noise due to numerical precision limitations.
Wavelet The wavelet kernel. There are many types of wavelet to choose from, the best choice is often the one that mimics the pattern of interests in the signal.
If you are unsure which one to choose, using the autotuning function will give you a good starting point.
See this video to learn more about the DWT.
Graphs
Filter response - If filtering is enabled, and order is non-zero, then the frequency response of the filter is shown. This shows how much attenuation there will be across the frequency spectrum.
After filter - Shows the current window after filtering is applied (in the time domain).
Spectral power - Shows power vs. frequency as computed by the chosen FFT size. Power is either linear or log based on settings. This is shown if the selected analysis type is FFT.
Wavelet function - Shows the wavelet kernel function. This is shown if the selected analysis type is Wavelet.
Wavelet approximation - Shows the approximation of the signal at the highest decomposition level. This is shown if the selected analysis type is Wavelet.
Output features of the spectral analysis block
Using FFTs:
The spectral analysis block generates 2 types of features per axis/channel:
Statistical features
RMS
Skewness
Kurtosis
Spectral features
Maximum value from FFT frames for each bin that was not filtered out
Note that the standard deviation is not calculated because when the mean is subtracted from a signal, the RMS equals the standard deviation.
The total number of features will change, depending on how you set the filter and FFT parameters.
For example, let's consider an input signal sampled at 62.5 Hz with 3 axis and the following parameters:
Low-pass filter
Filter cutoff set to 3 Hz
The number of generated features per axis is:
3 values for statistics (RMS, Skewness, Kurtosis)
1 value for the FFT bin capturing 1.95 to 5.86 Hz
With 3 axes/channels, that gives us a total of 12 features generated in total for the input signal.
Using Wavelets:
The Wavelet block implements the discrete wavelet decomposition plus feature extraction and dimensionality reduction. After decomposition, 14 features are calculated at each level:
Entropy
Zero cross
Mean cross
5 percentile
25 percentile
75 percentile
95 percentile
Median
Mean
Stdev
Variance
RMS
Skewness
Kurtosis
For example, for a 4-level decomposition, with 14 features per component, it will generate 70 features in total.
Last updated
