Anomaly detection (GMM)
Neural networks are powerful but have a major drawback: handling unseen data, like new gestures, is a challenge due to their reliance on existing training data. Even entirely novel inputs often get misclassified into existing categories. Gaussian Mixture Models (GMMs) are clustering techniques that we can use for anomaly detection. GMMs can perform well with datasets that would otherwise perform poorly with other anomaly detection algorithms (like K-means).
Not available for Community Projects
View our pricing for more information.
Gaussian Mixture Model (GMM)
A Gaussian Mixture Model represents a probability distribution as a mixture of multiple Gaussian (normal) distributions. Each Gaussian component in the mixture represents a cluster of data points with similar characteristics. Thus, GMMs work using the assumption that the samples within a dataset can be modeled using different Gaussian distributions.
Anomaly detection using GMM involves identifying data points with low probabilities. If a data point has a significantly lower probability of being generated by the mixture model compared to most other data points, it is considered an anomaly (this will output of a high anomaly score).
Looking for another anomaly detection technique? See Anomaly detection (K-Means)
GMM has some overlap with K-means, however, K-means clusters are always circular, spherical or hyperspherical when GMM can model elliptical clusters.
Features importance (optional)
In most of our DSP blocks, you have the option to calculate the feature importance. Edge Impulse Studio will then output a Feature Importance list that will help you determine which axes generated from your DSP block are most significant to analyze when you want to do anomaly detection.
See Processing blocks > Feature importance
Setting up the Anomaly Detection (GMM) learning block
The GMM anomaly detection learning block has two adjustable parameters: the Number of components and The axes.
Number of components
The number of (gaussian) components can be interpreted as the number of clusters in Gaussian Mixture Models.
How to choose the number of components?
When increasing the number of (Gaussian) components, the model will fit the original distribution more closely. If the value is too high, there is a risk of overfitting.
If you have prior knowledge about the problem or the data, it can provide valuable insights into the appropriate number of components. For example, if you know that there are three distinct groups in your data, you may start by trying a GMM with three components. Visualizing the data can also provide hints about the number of clusters. If you can distinguish several visible clusters from your training dataset, try to set the number of components as the number of visible clusters
Axes
The different axes correspond to the generated features from the pre-processing block. The chosen axes will use the features as the input data for the training.
Click on the Select suggested axes button to harness the results of the feature importance output.
Train
Click on Start training to trigger the learning process. Once trained you will obtain a view that looks like the following: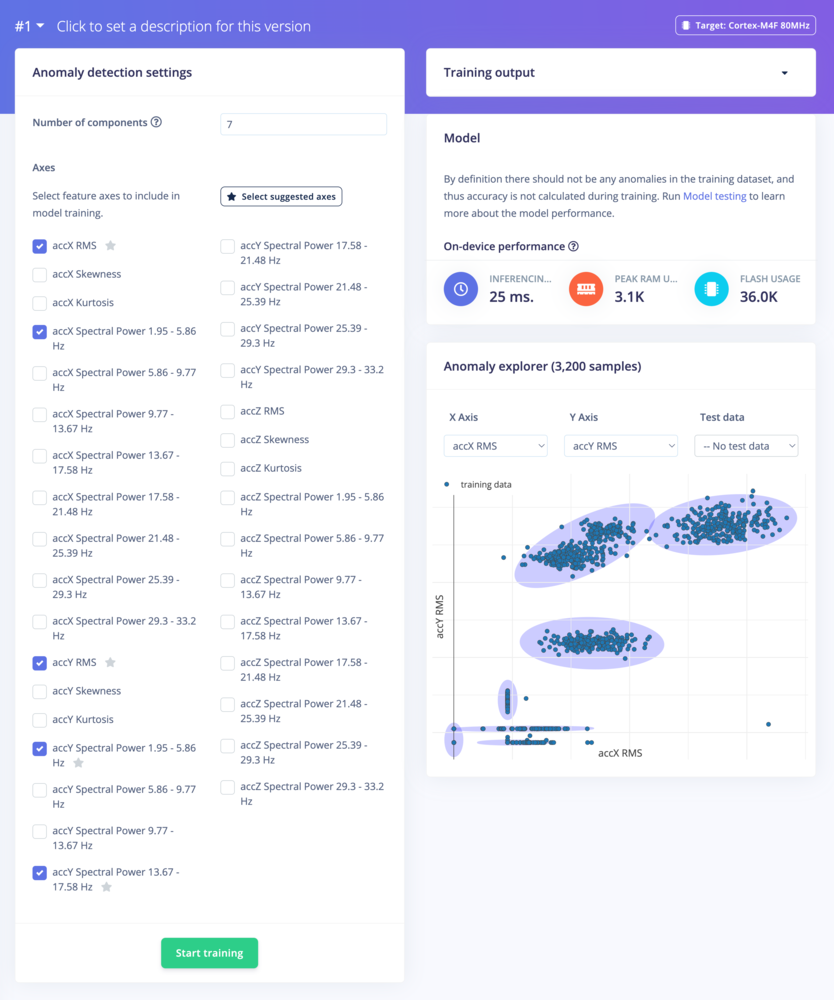
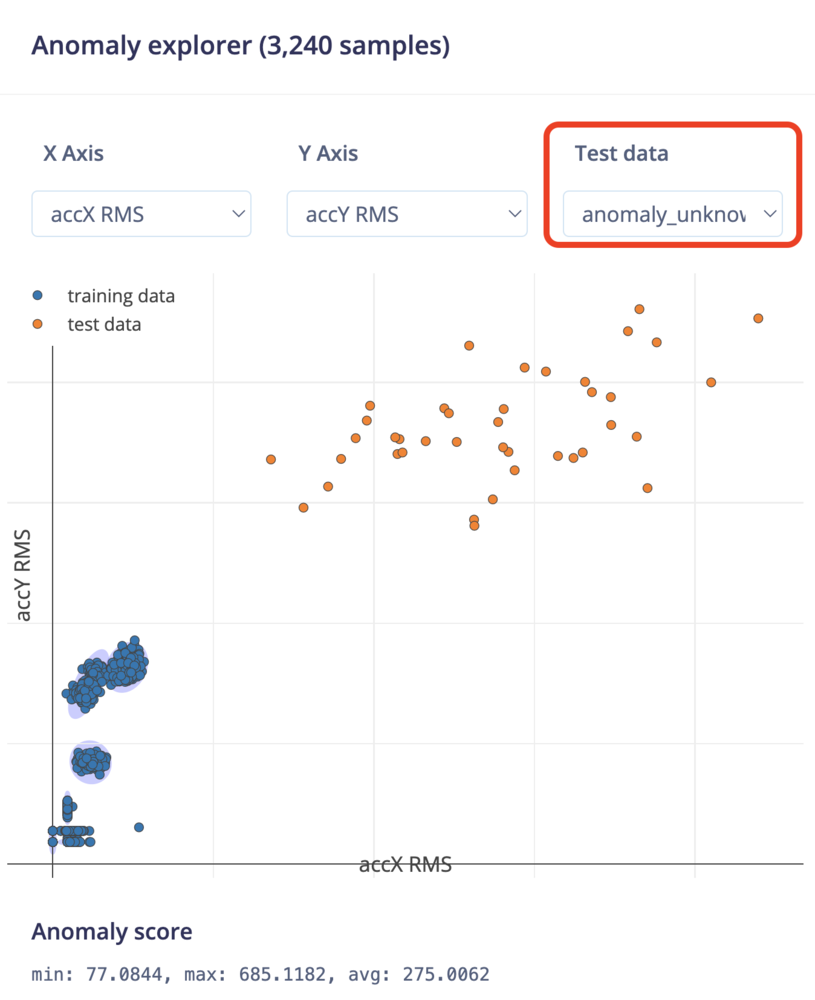
Note: By definition, there should not be any anomalies in the training dataset, and thus accuracy is not calculated during training. Run Model testing to learn more about the model performance. Additionally, you can also select a test data sample in the Anomaly Explorer directly on this page.
Testing the Anomaly Detection (GMM) learning block
Navigate to the Model testing page and click on Classify all: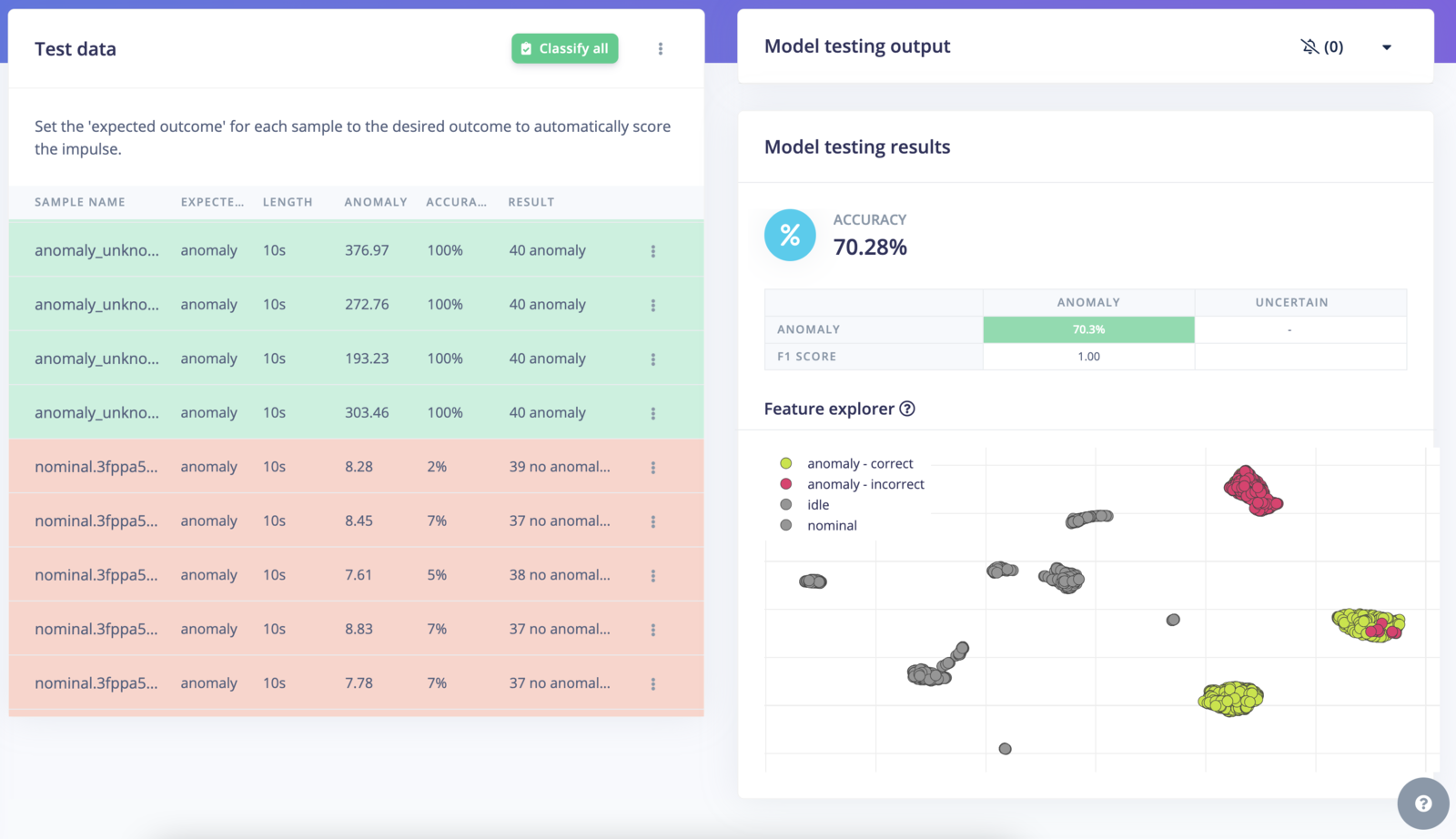
Limitation
Make sure to label your samples exactly as anomaly or no anomaly in your test dataset so they can be used in the F1 score calculation. We are working on making this more flexible.
Confidence threshold
In the example above, you will see that some samples are considered as no anomaly while the expected output is an anomaly. If you take a closer look at the anomaly score for non anomaly samples, the range values are below 1.00:
To fix this, you can set the Confidence thresholds
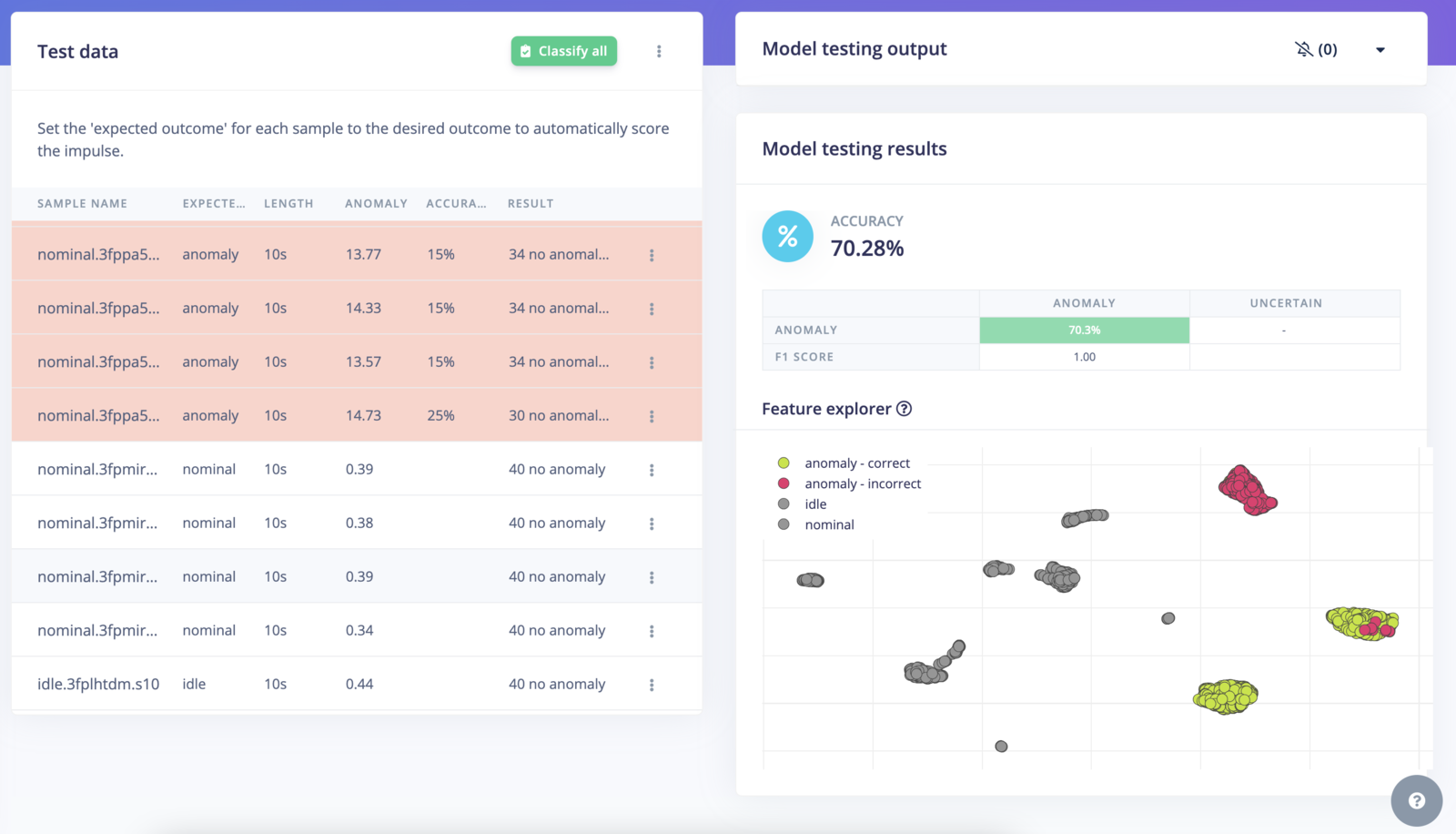
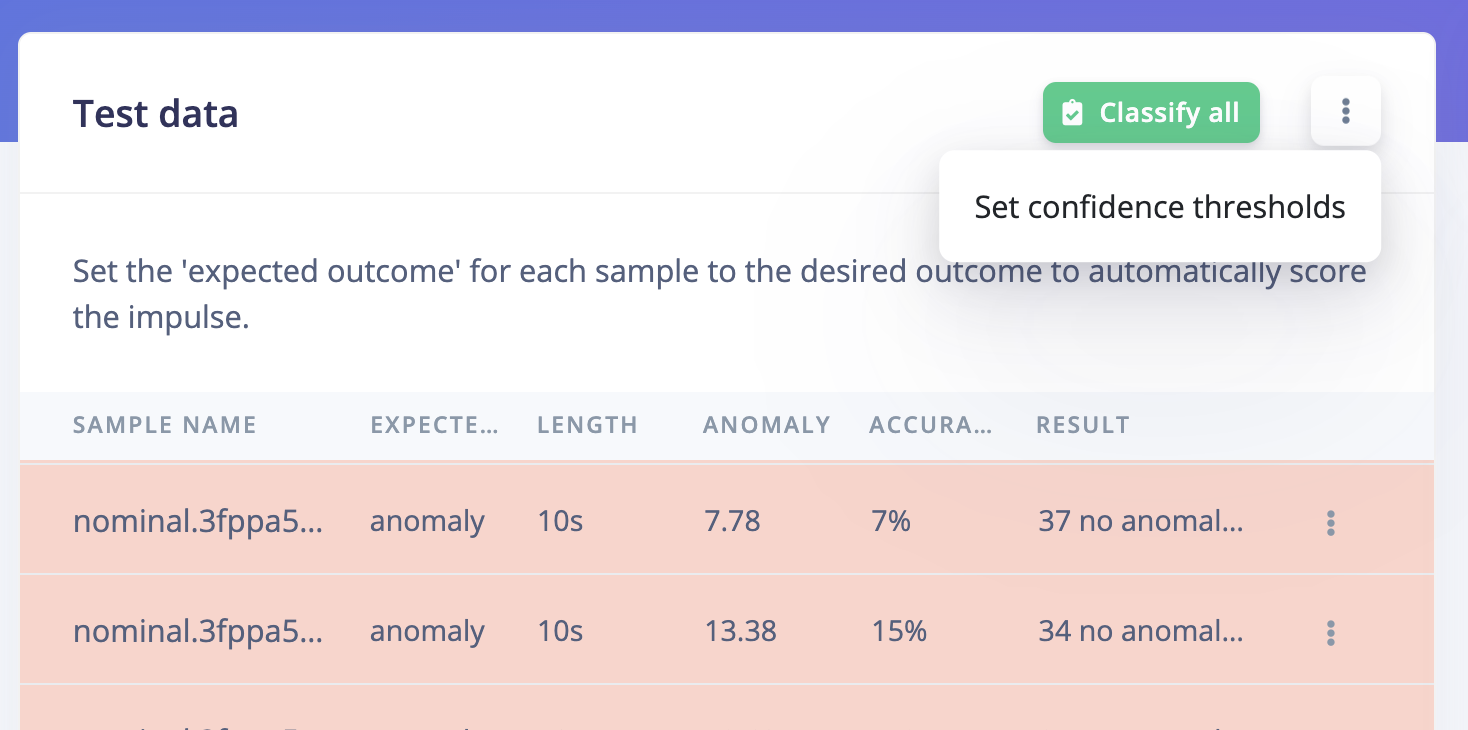
In this project, we have set the confidence threshold to 1.00. This gives results closer to our expectations:
Keep in mind that every project is different, please make sure to also validate your results in real conditions.
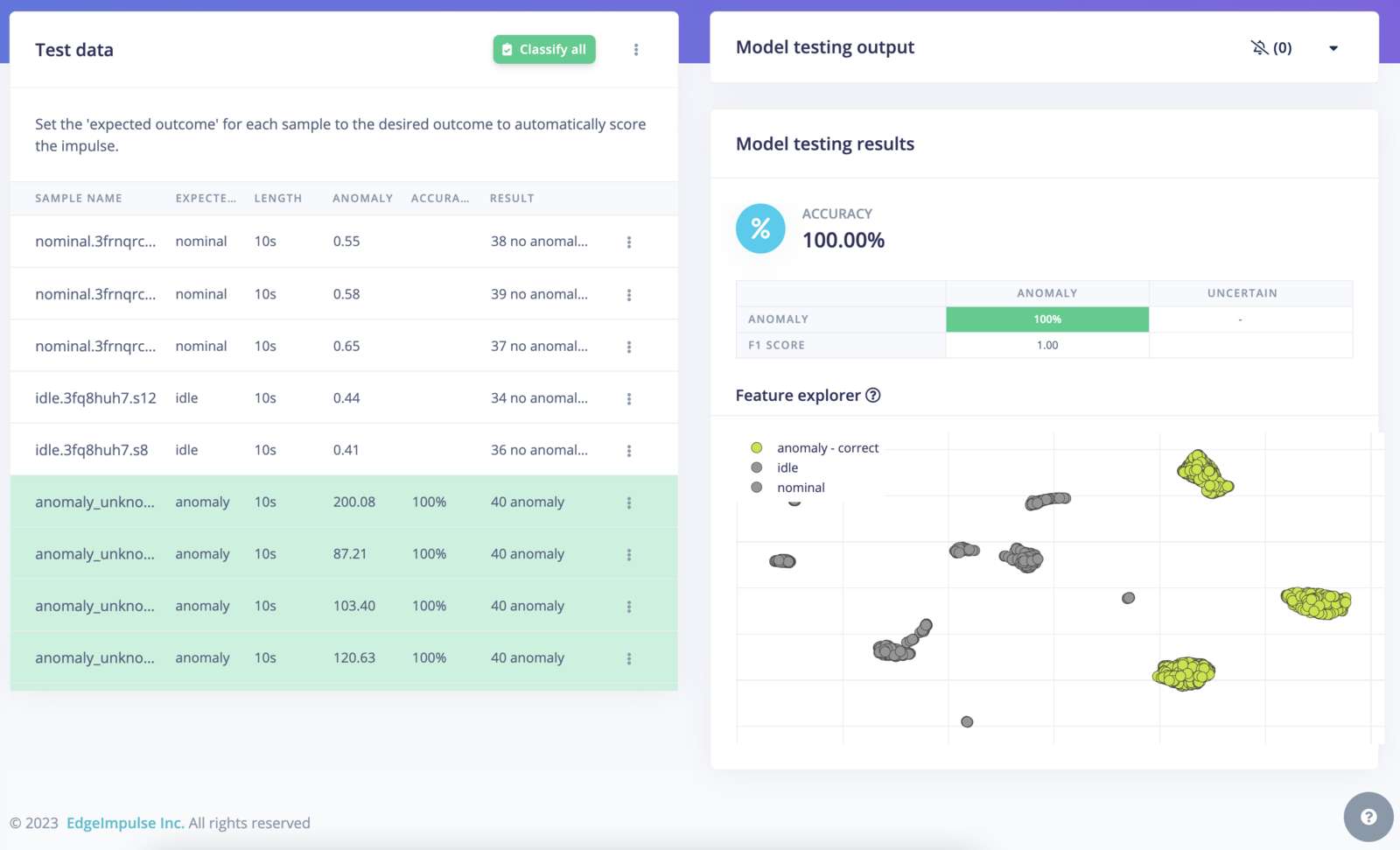
How does it work?
During training, X number of Gaussian probability distributions are learned from the data where X is the number of components (or clusters) defined in the learning block page. Samples are assigned to one of the distributions based on the probability that it belongs to each. We use Sklearn under the hood and the anomaly score corresponds to the
log-likelihood.For the inference, we calculate the probability (which can be interpreted as a distance on a graph) for a new data point belonging to one of the populations in the training data. If the data point belongs to a cluster, the anomaly score will be low.
Additional resources
Interesting readings:
Python Data Science Handbook - Gaussian Mixtures
scikit-learn.org - Gaussian Mixture models
Public Projects:
Last updated